Excerpt from Jazz Chords for Baritione Ukulele
There is geometry in the humming of the strings, there is music in the spacing of the spheres.
In Pythagoras’s day, around 500 BC in ancient Greece, there were stringed instruments called lyres. They were like mini-harps. They had no frets, but had seven or so strings that when plucked sounded good together. Those harmonies touched the early Greeks, and in them they saw clues to the movements of the heavens and the workings of the human soul.
Pythagoras, of mathematical fame, turned his scientific mind to trying to figure out why some tones sounded so harmonious together, and others didn’t.
He invented and used a monochord for his experiments, which, as the name implies, is one long single string stretched over a sound chamber. The string could be pressed down to experiment with the sounds created from different string lengths. Sometimes two were used together to see how two different string lengths sounded together.
Pythagoras was looking for mathematical relationships between the most harmonious of notes. He made some discoveries.
- The most harmonious note came from pressing the string in the middle. That is, when the ratio of the full string to the shortened section was 2:1. We know this today as an octave.
- The next most harmonious sound came from pressing 1/3 of the way down the string. That is, when the ratio of the full string to the shortened string was 3:2. We know this today as a fifth.
- And then, pressing 1/4 of the way down he found another wonderful harmony at the ratio of 4:3. This we know as a fourth.
Picking up your own stringed instrument you can repeat his observations.
- The 12th fret divides the string in 1/2, an octave.
- The 7th fret divides the string at the 2/3 point, a fifth.
- The 5th fret divides the string at the 3/4 point, a fourth.
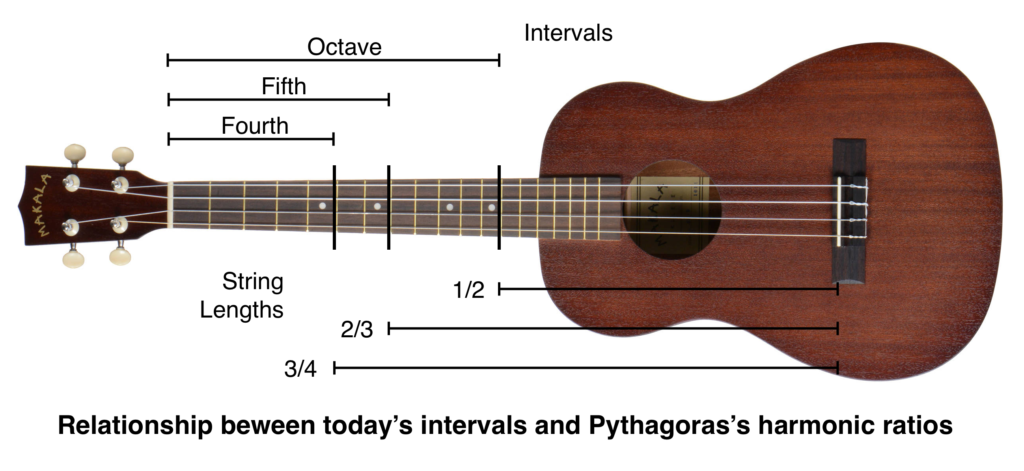
Remember, Pythagoras started with what sounded harmonious, and from that discovered the small integer ratios behind those harmonies. Those dots on the fretboard indicate that we, thousands of years later, still recognize the power of his observations.
Harmonics
There’s more magic in these intervals and it has to do with harmonics, or vibrations of a string. If one lightly damps a string in the middle and plucks it, it will sound an octave higher. The string vibrates then, not as one long string, but as two half length strings as shown in the diagram below.
Try it on the ukulele by holding your finger lightly over the 12th fret. It works best with the lower notes. When you find just the right spot you’ll hear a bell shaped tone, an octave above. (It helps to pluck cleanly and gently with a thumb nail to get that nice harmonic sound.)

You get the same effect by placing your finger over the seventh fret, thus dividing the string into vibrating thirds.
Holding your finger over the fifth fret, the 1/4 point, effectively cuts the string in half twice. In other words, creating a tone two octaves higher.
Clearly there is a special place for these ratios.
Pythagorean Scale
Full of the discovery of these simple ratios, Pythagoras set about developing a musical scale, a collection of notes that could be played at different positions on the monochord.
Step one was the octave. He drew a line on his monochord under the 1/2 way point, where our 12th fret is today. He wanted the scale to be within the octave.

He then based his first note on his favorite 3:2 harmonic ratio, and drew a line 1/3 way down the full string. This is where our 7th fret is today, and is where the 5th note of a major scale is played.

Now comes the clever part. He decided that the 3:2 ratio was the key to harmony and so he was going to continuously use it to find more notes in his scale. Thus, he went down 1/3 of the way from his new note, and made another mark. This brought the playable part of the string to 4/9 of the original string: 2/3 x 2/3 if you remember fractions and math (Pythagorus was good at this stuff). It’s our 14th fret.

But that’s out of range of the octave. What to do? Well simply lower it an octave to bring it back. How is that done? By making it twice as long, which is 2 x 4/9 = 8/9. He made another line. That is our 2nd fret.

And so on, he continued this laborious process, with increasingly complex fractions until, miracles of miracles, after the 12th note he was at the next octave. He had gone full circle.
Pythagoras had thus invented the 12 chromatic notes of the Western musical scale, deriving them from a cascading sequence of beautifully harmonious 3:2 ratios, or, as we call them, fifths.
His work is most obvious on stringed instruments, where the frets correspond to our notes and his simple ratios. Have you noticed how the frets get closer as you move up the neck? No matter which fret you start on, if you go up 12 frets you divide the string in half, up 7 frets finds the 2/3 mark, and 5 frets the 3/4 mark. Harmonious.
You’ve probably heard of the Circle of Fifths, and it’s sometimes explained as a pattern in the scale, but it’s really the other way around. Pythagoras circled the fifths and invented the scale.
Epilog — It worked out beautifully, almost, well not quite. The perfect fifths didn’t exactly converge on an octave as I said and as Pythagoras had hoped. It was close, but not perfect. To make it work, some intervals had to be shortened, which was okay if it was an interval not used in a particular key. But if one wanted to play in different keys, or build an instrument like a piano with fixed pitches, or a baritone ukulele with frets… musicians from the Renaissance on kept experimenting with very small adjustments, temperaments, to the intervals trying to get something that played the same in every key.
They finally did, and that’s the actual scale and the precise spacing of frequencies that we have today. Still, a musician with a sensitive ear and a fretless instrument, like the violin, will sometimes play those perfect harmonies that so moved Pythagoras.
Music of the Spheres
Pythagoras and other Greeks of the day spent their evenings under the full splendor of the Milky Way, pondering the motions of the stars, planets and moon. When Pythagoras found that simple integer ratios were the key to musical harmony, well isn’t it obvious that those simple ratios also explained the motions and harmony of the cosmos as well?
They called this idea the Music of the Spheres.
Which brings us to a jazz classic based on the Circle of Fifths—Fly Me to the Moon.
